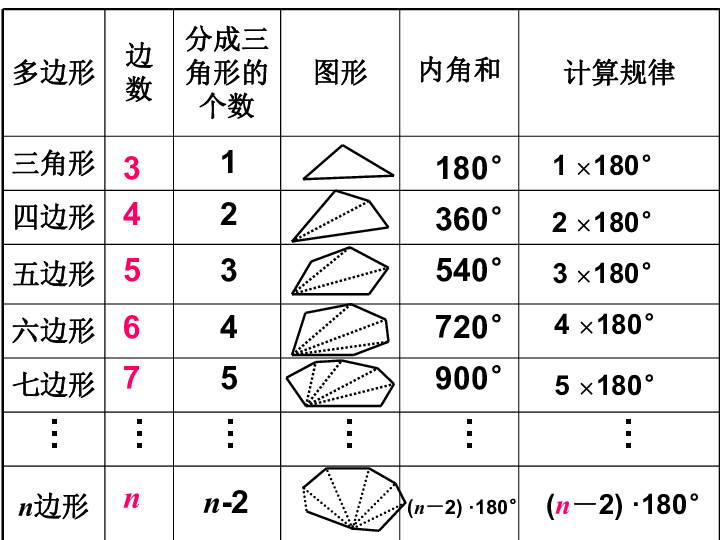
分子は多角形の内角の和を出す計算ね。 上に載せた記事で 説明はしてある。 そしてそれを3で割る。 もちろんこの3は三角形だから。 そうすれば60度と答えが出る。 ok? で、今回の問題は160度っていってるでしょ? じゃあこの写真みたいに 計算してみよう。以上のことから、多角形の内角の和は下の 公式 で求められます。 多角形の内角の和 = 線を引いて現れた三角形の数 × 180 これをもっと簡単な公式にします。 上の図をると、三角形の数は多角形の角の数より2つ少ないことがわかります。対角線の本数の公式 \(n\) 角形の対角線の本数を求める公式があります。 \(n角形の対角線の本数=(n3)×n÷2\) もちろんこの公式は暗記して欲しいのですが、たまにしか利用しない公式なので よほど熱心に暗記しないと、すぐに忘れてしまいます。 この公式は、「なぜこの公式になるのか」を理解
这张初中数学公式表来得太及时了 初一到初三都能用 速收藏 爱子网
多角形 内角 公式
多角形 内角 公式-星形多角形の内角 星形多角形 2 星形五角形の角の和を求めよう(∠a+∠b+∠c+∠d+∠e) 下の図のように,多角形の各辺を延長していくと,何回か交わったあと交わらなくなります。 このときにできる図形を星形多角形といいます。N角形の内角の和=180×(n-2) この公式を忘れてしまったらどうしたらよいでしょうか? 多角形の内角の和は求められないでしょうか? そんなことはありません。 忘れてしまった場合は、前項で使用したこんな表を自分で作成してみましょう。


16下半年数学教师资格证面试真题 精选
内角の和の公式!内角の和が1800°の多角形は何角形? 中学 次は2700。(オンライン整数列大辞典の数列 A) 1800 = 2 × 30 2 n = 30 のときの 2n 2 の値とみたとき1つ前は16、次は1922。2-4-1 星型多角形の内角の和 教材(問題場面) 図のように5つの点A,B,C,D, Eがある。多角形を三角形に分けて、内角を考えます。 予習シリーズ28ページの公式の成り立ちについて、図をよく見ながら理解を進めてください。 公式 「180×(N-2)=N角形の内角の和」 により、180×(7-2)=900となるので、七角形の内角の和は、900度です。
内角の和の公式!内角の和が1800°の多角形は何角形? 中学 次は2700。(オンライン整数列大辞典の数列 A) 1800 = 2 × 30 2 n = 30 のときの 2n 2 の値とみたとき1つ前は16、次は1922。クロシロです。 ここで扱う問題、数字は私が独自に作成してるため引用などは行っておりません。 高校入試でどこの都道府県でも出題される確率が高い図形の証明があると思います。 今回は、図形の証明を解くカギにもなる 覚えておくべき角度の知識をおさらいしていこうと思います。以上のことから、多角形の内角の和は下の 公式 で求められます。 多角形の内角の和 = 線を引いて現れた三角形の数 × 180 これをもっと簡単な公式にします。 上の図をると、三角形の数は多角形の角の数より2つ少ないことがわかります。
クロシロです。 ここで扱う問題、数字は私が独自に作成してるため引用などは行っておりません。 高校入試でどこの都道府県でも出題される確率が高い図形の証明があると思います。 今回は、図形の証明を解くカギにもなる 覚えておくべき角度の知識をおさらいしていこうと思います。多角形の内角の和と対角線の数の問題です。 公式を覚えておけば出来ますが、最近は公式の導き方を問うことも増えています。 丸暗記するのではなく、多角形の性質をしっかり確認して公式を使うようにしていきましょう。 多角形の内角のクロシロです。 ここで扱う問題、数字は私が独自に作成してるため引用などは行っておりません。 高校入試でどこの都道府県でも出題される確率が高い図形の証明があると思います。 今回は、図形の証明を解くカギにもなる 覚えておくべき角度の知識をおさらいしていこうと思います。



初中数学全部公式大全 冲刺满分必备 星火网校



如何 多边形几何 五边形 六边形和十二边形 21
正多角形の内角(外角)の求め方とは 正多角形とは、 「すべての辺の長さが等しく、すべての内角の大きさが等しい多角形」 を指します。 よって、多角形の内角の和の公式より、正多角形の一つ一つの内角は$$\frac{180°×(n2)}{n}$$と求めることができます。「多角形の外角の求め方」 を学習しよう。 前回は、n角形の内角の和の公式「180°×(n-2)」という公式を覚えたよね。 今度は多角形の外側の角、「外角」はどうなるのか見てみよう。 実は、外角の方がシンプルな公式になっているんだよ。はい! じゃあ、五角形の内角の和を出して〜 え? 公式忘れたから解けない? ちょいちょい。 そんなんで諦めるの??? 待って それは早すぎ!! 三角形の内角の和はさ〜 180度でしょ?



初中几何多边形内角和问题的求解技巧 就看你公式能不能灵活应用 每日头条


凹5多边形内角和网友说凹多边形也可以套 N 2 180 这个公式 怎么套阿 Ps 请把图画出来 最好电子版 如果必须手画 Lz也不介意 作业 慧海网
多角形の内角の和は、下記の公式で算定します。 多角形の内角の和=180×( n-2) nは多角形の辺の数です。多角形のnの値を下記に示します。 三角形 ⇒ n=3 四角形 ⇒ n=4 五角形 ⇒ n=5 六角形 ⇒ n=6 つまり「〇角形」の〇部分がnに相当する値です。正多角形の内角(外角)の求め方とは 正多角形とは、 「すべての辺の長さが等しく、すべての内角の大きさが等しい多角形」 を指します。 よって、多角形の内角の和の公式より、正多角形の一つ一つの内角は$$\frac{180°×(n2)}{n}$$と求めることができます。N角形の内角の和を180°×(n-2)の公式としてまとめるときに,対角線を引い ねらい て三角形の数(n-2)を求めるだけでなく,線を引く出発点を変えるだけで三角形の 数がかわってくることに気づかせる。そして,三角形の数が変わっても一般形が180°



多角形の内角の和 一覧表と簡単公式による求め方 Yattoke 小 中学生の学習サイト


多边形内角和教案 Doc 十八文库
数学の質問です。多角形の内角の和を求める公式はなぜ 180°×(n-2)となるのでしょうか。 あと、多角形の外角の和はなぜ360°なのでしょうか。 長文になりましたが、分かる方説明よろしくお願いします。四角形なら180°が2つだから360° 五角形なら180°が3つだから540° 六角形なら180°が4つだから7° ・・・ って、線を引いたら三角形ができるので、180°がいくつあるかでその多角形の内角の和を求めることができますⅠ 面積の公式 1辺 \(~a~\) の正四角形(正方形)の面積の公式は誰でも知っていますが、正三角形の面積の公式は答えられない人が多いのではないでしょうか。 しかし、正三角形は定期テストや入試でよく登場する図形であり、面積が必要となる場面も少なくありません。



ユニーク三角形角度公式 ただぬりえ



八年级下册数学沪科版第十九章第一节 多边形内角和 教案 莲山课件
数学・算数 多角形の内角の求め方が分かりません。 教科書には「180°×(n-2)」とあるのですが、この式の意味がよく分かりません。 「(n-2)」とはどこから来ているのでしょうか? 宜しくお 質問Noクロシロです。 ここで扱う問題、数字は私が独自に作成してるため引用などは行っておりません。 高校入試でどこの都道府県でも出題される確率が高い図形の証明があると思います。 今回は、図形の証明を解くカギにもなる 覚えておくべき角度の知識をおさらいしていこうと思います。出典 フリー百科事典『ウィキペディア(Wikipedia)』 ( 59 UTC 版) 面積公式 多角形の面積は、頂点の位置ベクトルから外積を用いて計算することができる。 多角形の頂点を反時計回りに並べて、それらの位置ベクトルを →, , → とすると、その面積は ∑ = → →


多边形内角和外角和 多边形外角公式 多边形的内角和 多边形外角



八年级数学公式 四边形公式 初二数学公式总结 求学网
5角形までの内角の和は覚えましょう。多角形の内角の和は下の公式で求められます。 角形の内角の和 = 180 × ( 2) 例えば8角形の内角の和は 180 × (8 2) = 1080 と求めます。 内角の和から 角形の を求める多角形を三角形に分けて、内角を考えます。 予習シリーズ28ページの公式の成り立ちについて、図をよく見ながら理解を進めてください。 公式 「180×(N-2)=N角形の内角の和」 により、180×(7-2)=900となるので、七角形の内角の和は、900度です。


一个五边形最少能分成几个三角形 热备资讯



课题 探索多边形的内角和下载 Word模板 爱问共享资料


这张初中数学公式表来得太及时了 初一到初三都能用 速收藏 爱子网



初二数学人教版 多边形内角和定理知识点总结 三好网


正多边形内角 正多边形内角度数知道正多边形的内角度数怎么求它是几条边 尚书坊


六边形 头条百科


为什么瓷砖可用三角形 正方形 正六边形平铺而别正多边形不行 新闻 蛋蛋赞



Codeforces 659d Bicycle Race 多边形内角和公式 3 Csdn博客



如何利用编程机器人程小奔编程玩几何 Makeblock


对多边形内角和公式的探究 9 2多边形的内角和与外角和 初中华师大版13版 数学中国网 Mathschina Com


凹多边形图片 第1页 要无忧健康图库



北师大版八年级下册 多边形的内角和 优秀公开课教案设计下载 Doc 文档铺



Python Turtle 画正多边形和多角形 弄斧人y Y的博客 Csdn博客 用python画正五边形的代码



多边形内角和案例分析下载 Word模板 爱问共享资料


人気ダウンロード 正12角形内角 壁紙引用画像hd


数理天地



凹多边形内角和公式 多边形及其内角和素材 多边形内角和ppt 多边形的内角和教学素材 Www Dingjisc Com



正多边形和圆公式
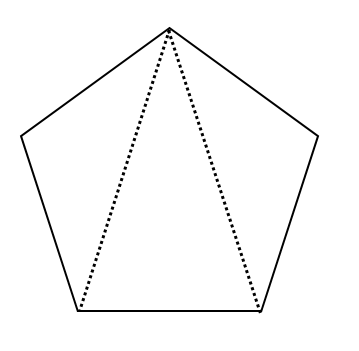


正五边形的内角和是 时习社区


初三数学多边形内角和公式知识点总结 初三网



初二数学复习重点之三角形全攻略



联系生活 情景导入 Ppt Download


学霸都在看的初中数学公式归纳 新学期能派上大用场 雪花新闻


16下半年数学教师资格证面试真题 精选



多角形の内角の和の公式を3通りの方法で証明する 具体例で学ぶ数学


多边形内角和公式 跟着mo学习gis 本地网站大全
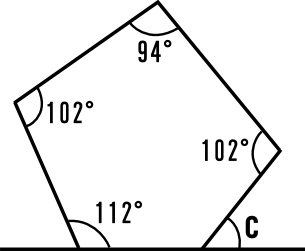


いろいろ多角形内角和 リタ ベルナル



凹多边形外角和公式 三人行教育网 Www 3rxing Org
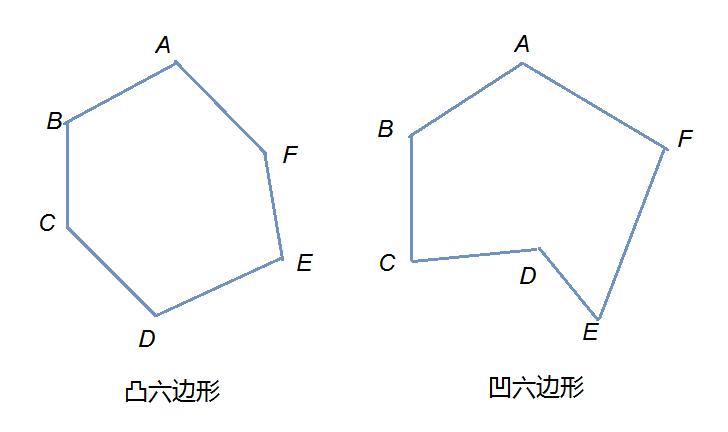


六边形 搜狗百科



表面上简单的18石家庄中考填空压轴题 知乎



如何 多边形几何 五边形 六边形和十二边形 21



正多边形和圆公式



初中数学 公式定理大全 赶快收藏学习 3 经验 辣妈女性网
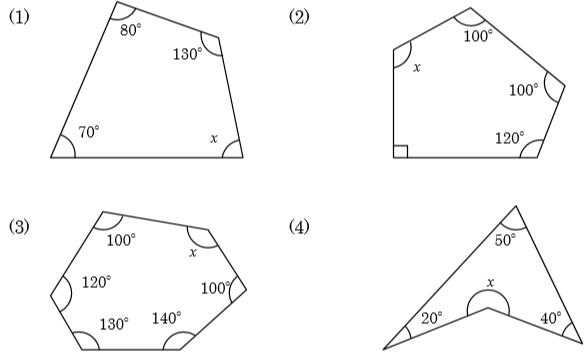


内角和公式 五边形内角和 多边形的外角和 N边形的内角和是


第23讲总复习 正多边形与圆有关的证明和计算 提高 长沙百分罗物理工作室


农村中小学现代远程教育资源



表面上简单的18石家庄中考填空压轴题 知乎


教师资格面试数学试讲 多边形的内角和 试讲稿 答辩 安徽山香教育



直角锥体积 表面积 侧面积 计重 报价计算公式与在线计算器 三贝计算网 23bei Com



多边形的内角和



八年级数学下册6 平行四边形课题多边形的内角和与外角和学案 新版 北师大版 Doc 在线文库www Lddoc Cn 在线文库www Lddoc Cn


超全初中几何图形知识点归纳 快来收藏
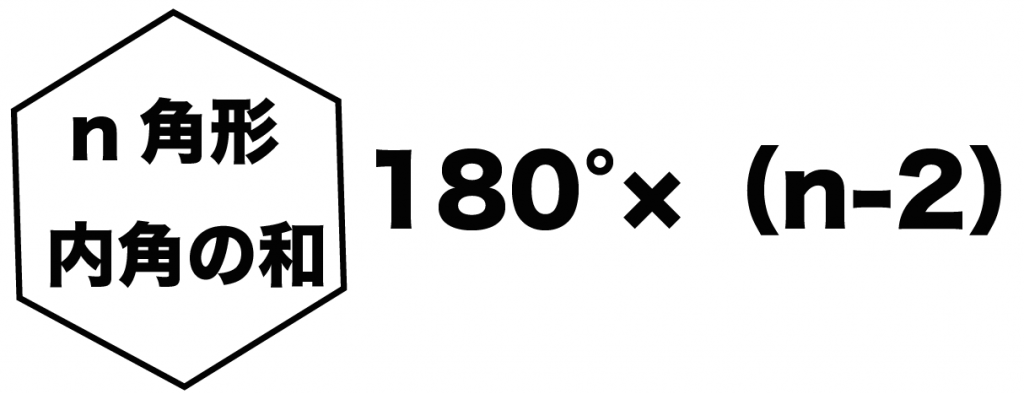


中2数学 多角形の内角の和が3秒でわかる公式 Qikeru 学びを楽しくわかりやすく


教师资格面试数学试讲 多边形的内角和 试讲稿 答辩 安徽山香教育


Education Ti Com Sites China Downloads Activities Translated Geometry Quadrilaterals And Polygons Sum Of Exterior Angles Of Polygons Teacher Pdf



最全初中数学公式表 初一到初三都能用 楠木轩



多边形外角和和内角和的关系 三人行教育网 Www 3rxing Org



内角和公式和外角和公式 多边形外角公式 多边形的内角和 多边形外角



内角の和の公式 内角の和が1800 の多角形は何角形 中学や高校の数学の計算問題


多边形内角和公式的推导及应用 16 1多边形 初中京教版13版 数学中国网 Mathschina Com


正九边形求内角 腾讯视频
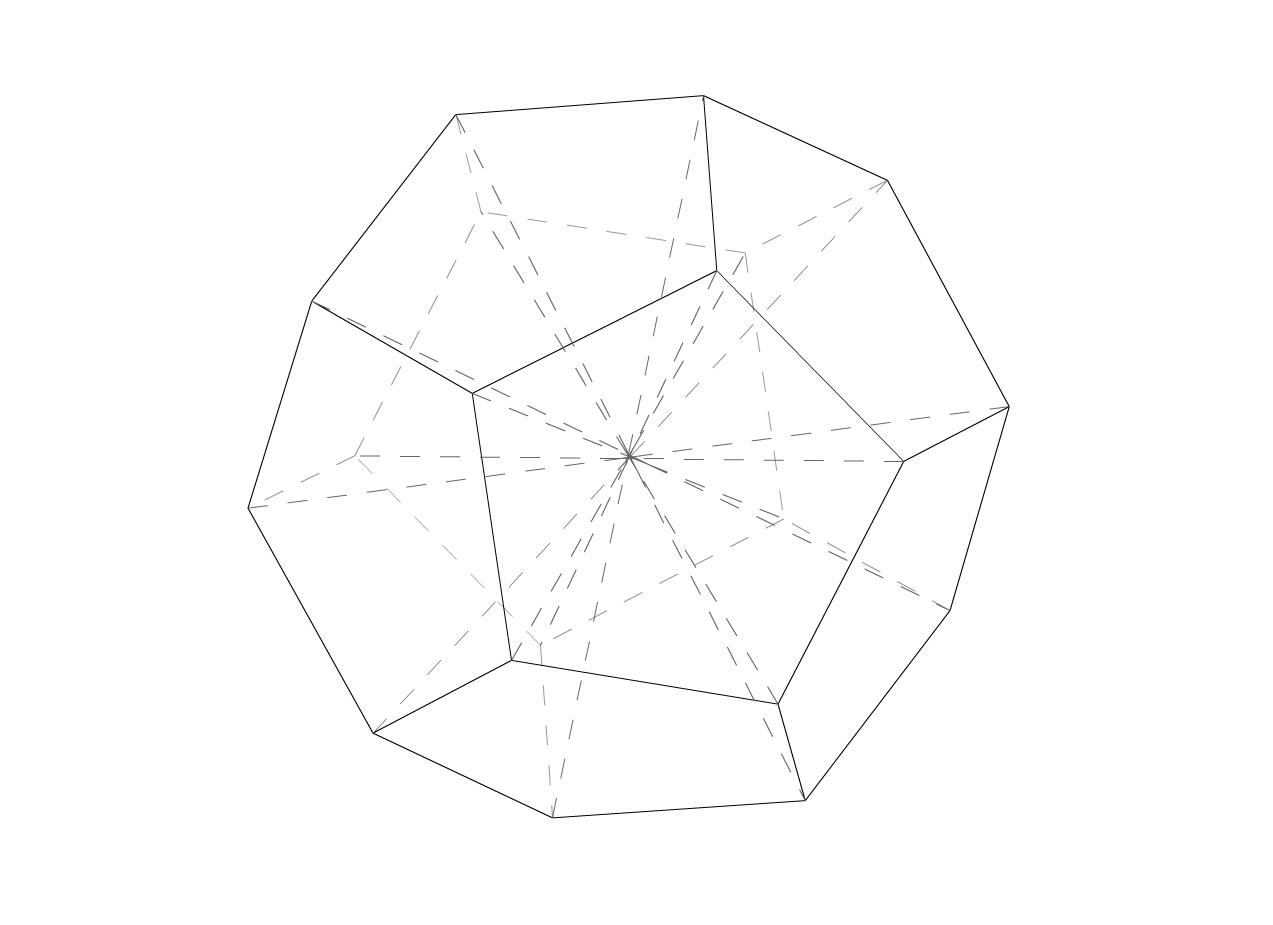


人気ダウンロード 正12角形内角 壁紙引用画像hd



初中几何多边形内角和问题的求解技巧 就看你公式能不能灵活应用 每日头条


毕克定理的公式毕克定理怎么证明 朵拉利品网


Education Ti Com Sites China Downloads Activities Translated Geometry Quadrilaterals And Polygons Sum Of Exterior Angles Of Polygons Teacher Pdf



五边形内角和 五边形内角和 六边形内角和 N边形内角和 圆周率 五边形 多边形内角和 五边形内角 五边形内角和是多少度 万能公式 五边形的内角和 淘书楼图库


2



多边形内角和比它的外角和3倍少180 怎么求多边形边数 哔哩哔哩 つロ干杯 Bilibili


14初三数学三角形多边形内角和外角和



新しい六角形内角 壁紙配布
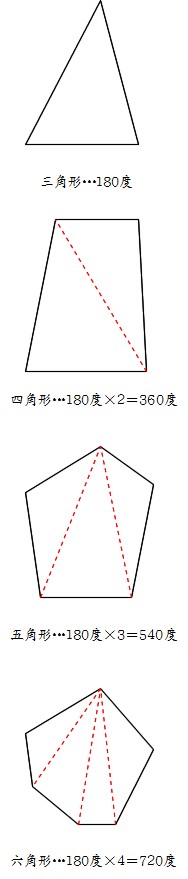


Math 多角形の内角の和 働きアリ



任意多边形内角和 三人行教育网 Www 3rxing Org



二简单多面体的欧拉公式 人教版高中数学选修3 3 高中课本 中学课本网
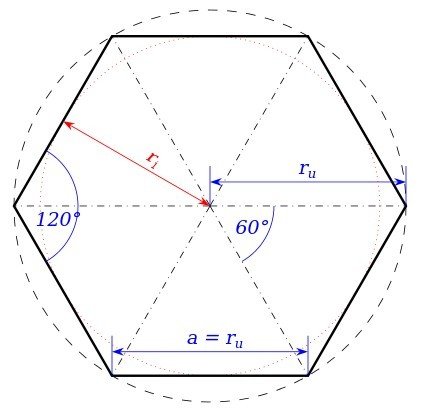


六边形 360百科


从不同方向看



课题 探索多边形的内角和下载 Word模板 爱问共享资料
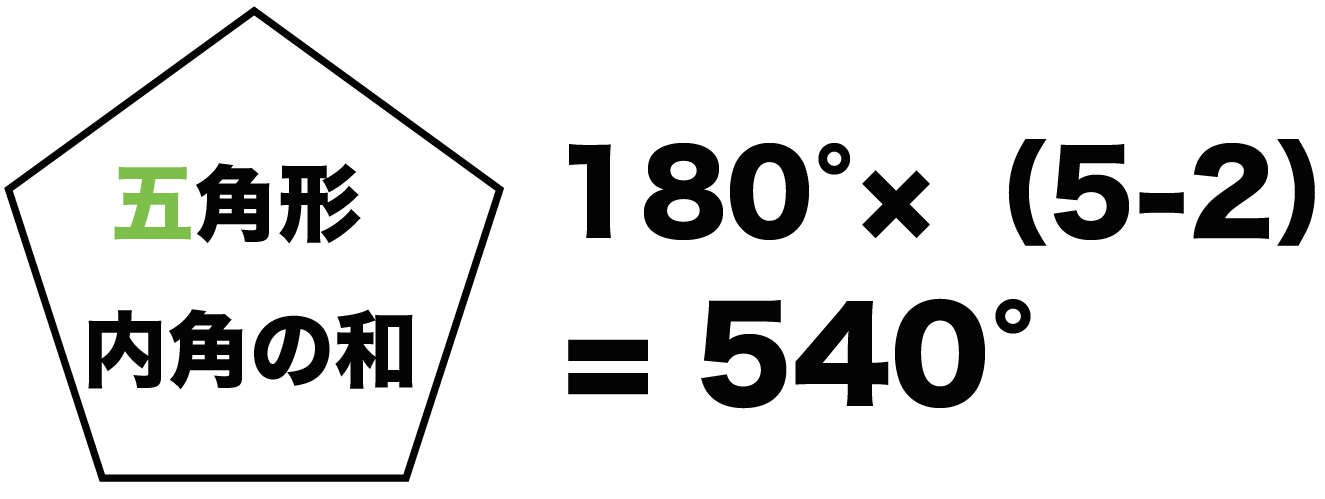


中2数学 多角形の内角の和が3秒でわかる公式 Qikeru 学びを楽しくわかりやすく


内角和公式 五边形内角和 多边形的外角和 N边形的内角和是



五边形内角和 五边形内角和 六边形内角和 N边形内角和 圆周率 五边形 多边形内角和 五边形内角 五边形内角和是多少度 万能公式 五边形的内角和 淘书楼图库


数理天地



多角形の内角の和 一覧表と簡単公式による求め方 Yattoke 小 中学生の学習サイト


正多边形内角和多边形内角和公式推导方法 尚书坊



内角和外角 维基百科 自由的百科全书


八上数学 多边形的内角和 练习题 Doc 十八文库



八年级数学上册新人教版第十一章第三节多边形及其内角和第二课时 多边形的内角和 教案 莲山课件


一课研究之 三角形的内角和 差异



新しい六角形内角 壁紙配布


教学反思 探索多边形内角和 600字 范文118


多边形内角和公式证明的多种方法 桂军民数学 新浪博客


いろいろ多角形内角和 リタ ベルナル



任意五边形内角和是多少 三人行教育网 Www 3rxing Org


多边形对称轴公式


初中数学难题新题精讲精练300例 第2版



外角和公式示意图 第1页 一起扣扣网



八年级上册第十一章 三角形 简介


五边形 维基百科 自由的百科全书


多边形及其内角和教学设计 多边形及其内角和教学设计资料 新学语文网



初中几何多边形内角和问题的求解技巧 就看你公式能不能灵活应用 每日头条


凹多边形图片 第1页 要无忧健康图库



多边形内角和推导图片 第1页 一起扣扣网



0 件のコメント:
コメントを投稿